알고리즘/백준

[Java] 백준 배열 돌리기

문바리 2022. 8. 16. 21:39
728x90

1. 문제 분석

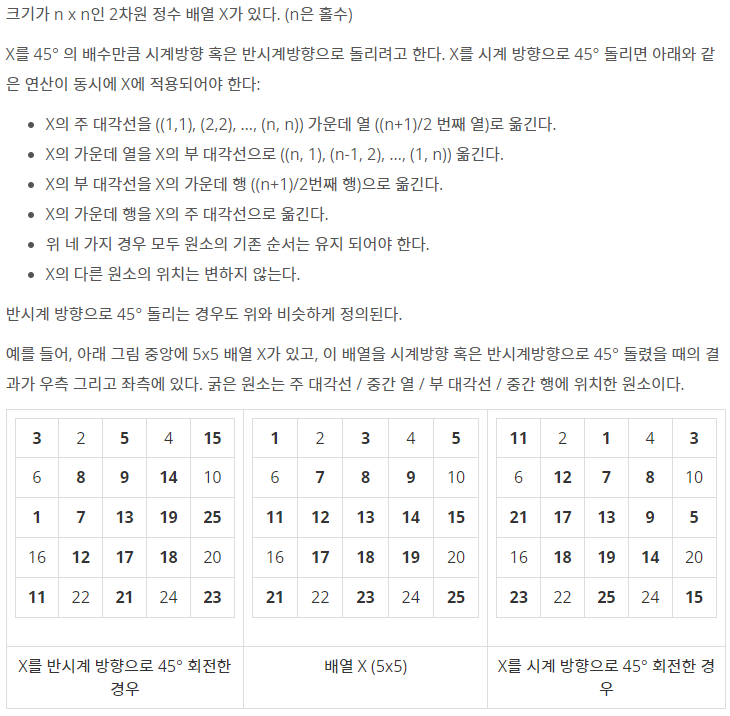
배열을 주어진 각도로 45도씩 돌리는 것이다. 이런 문제는 반드시 규칙이 존재한다.

예시로 보는거는 이해하는데 조금 어려우니 밑의 표를 보고 이해해보자.

각 대각선을 그려보면 다음과 같이 나온다.

각 번호는 다음과 같이 이동한다.

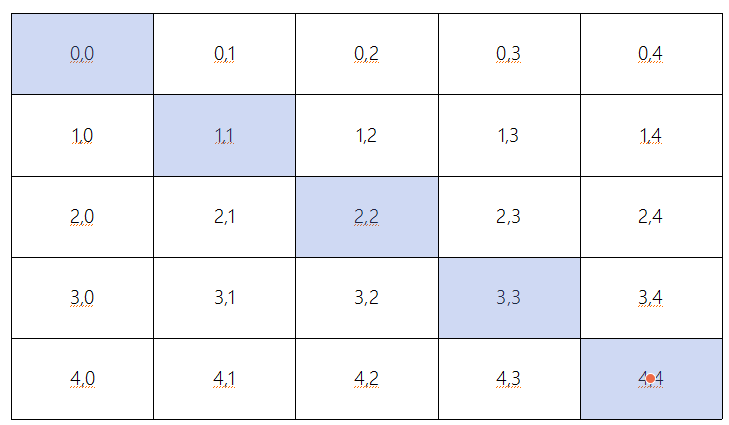
먼저 색칠한 부분의 영역을 움직여보자. 왼쪽 그림은 오른쪽 그림으로 변화해야한다.

여기서 볼 점은 바뀐 자리의 가로 인덱스는 2, 가운데가 된다. 또한 모두가 2로 동일하다.

세로 인덱스는 0 ~ 4로 증가한다. 결과적으로 arr[k][arrSize/2] = arr[k][k]가 된다.

(바뀌는 자리가 오는 것이다. 절대 헷갈리면 안된다.)

 

이번에도 왼쪽이 오른쪽이 된다고 보자.

여기서 볼점은 전과 마찬가지로 세로가 고정이라는 점이다.

반면 오른쪽은 명확한 기준이 없어보인다. 하지만 잘 보면 배열의 우측 상단 끝에서 좌측 하단 끝으로 내려가는 것이다.

즉, arr[k][arrSize - 1 - k] = arr[k][arrSize/2] 가 된다. (배열이므로 1을 빼주었다.)

 

이런식으로 4개의 경우의 수를 구하면 된다. 2개는 직접 해보자.

2. 구현

import java.io.*;
import java.nio.Buffer;
import java.util.*;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int tc = Integer.parseInt(br.readLine());
        StringTokenizer st;
        for (int i = 0; i < tc; i++) {

            //input
            st = new StringTokenizer(br.readLine());
            int arrSize = Integer.parseInt(st.nextToken());
            int degree = Integer.parseInt(st.nextToken());

            int[][] arr = new int[arrSize][arrSize];
            int[][] copyArr = new int[arrSize][arrSize];

            for (int j = 0; j < arrSize; j++) {
                st = new StringTokenizer(br.readLine());
                for (int k = 0; k < arrSize; k++) {
                    arr[j][k] = Integer.parseInt(st.nextToken());
                    copyArr[j][k] = arr[j][k];
                }
            }
            //calc
            int calcDegree = 0;
            if (degree < 0) {
                degree += 360;
            }

            calcDegree = degree / 45;
            for (int t = 0; t < calcDegree; t++) {
                for (int k = 0; k < arrSize; k++) {
                    copyArr[k][arrSize / 2] = arr[k][k];
                    copyArr[k][k] = arr[arrSize / 2][k];
                    copyArr[k][arrSize - 1 - k] = arr[k][arrSize / 2];
                    copyArr[arrSize / 2][arrSize - 1 - k] = arr[k][arrSize - 1 - k];
                }
                for (int k = 0; k < arrSize; k++) {
                    for (int j = 0; j < arrSize; j++) {
                        arr[j][k] = copyArr[j][k];
                    }
                }
            }

            for (int[] info : arr) {
                String temp = "";
                for (int data : info) {
                    temp += data + " ";
                }
                System.out.println(temp);
            }
        }
    }
}

배열의 원상태에서 데이터를 가져와야하므로 copyArr를 사용했다. 단순히 원래 배열의 값을 가져와서 복사한 것이다.

반드시, 마지막에 옮긴 배열을 똑같이 복사해줘야 한다.

 

또한 degree를 보면 0 <= 절대값 x <= 360이다.

마이너스가 되면 반 시계로 가는 것인데 360을 구하면 양수값 그대로 계산이 가능하다.

3. 마무리

구현문제는 생각하는 것이 어렵지 구현은 쉽게 된다.

오히려 bfs, dfs같은 알고리즘 기법보다 쉬우니 천천히 생각해보자.

반응형